Encryption – Шифрування.
Частина перша. Шифрування алгоритмом RSA.
Розділ перший. Ліричний
RSA отримав свою назву за першими літерами його творців. Трьох геніяльних математиків Рівест (Rivest), Шамір (Shamir), Адлман (Adleman) – повністю Рівест Рональд Лінн, Шамір Аді, Адлман Леонард Макс відповідно. Ці імена соромно не знати якшо ви айтішник.
RSA шифрування ґрунтується на простих числах і спільних множниках і спільних дільниках з остачею (модулос). Це шифрування є АСИметричним. Текст ЗАшифровується публічним ключем, котрий отримали від свого – назовімо – респондента, з ким ви таємно листуєтесь через НЕ таємні канали, а ваш респондент РОЗшифровує ваше повідомлення своїм привантним ключем.
Коли ви генеруєте собі RSA “сертифікат”, він складається з двох частин, як ви здогадалися з попереднього абзаца – приватний ключ і публічний ключ. Приватний ключ належить вам і лише вам. Нікому його не показуйте. Він унікальний як відбиток пальця. Вашим приватним ключем ви можете ЛИШЕ РОЗшифровувати повідомлення зашифровані для вас за допомогою вашого, а не чийогось іншого, публічного ключа, котрий ви роздаєте всім кому завгодно. Його роздача всім – його публічність – на вашу безпеку ніяк не впливає.
Будь-хто, отримавши ваш публічний ключ, може зашифрувати цим ключем повідомлення, котре вже навіть він сам не зможе розшифрувати назад (хіба шо напише по пам’яті, чи якшо текст зберігся в звичайному відкритому файлі-чорновику на диску чи в буфері комп’ютера). Лише ВИ можете розшифрувати його за допомогою вашого приватного ключа, котрий ви було згенерували в парі з публічним.
Сприймайте це як звичайний навісний замок на коробці для посилок. Ключа до цього замка ви не маєте, але конструкція замка дозволяє защепити його скобу в корпус із зубчиком, стиснувши пальцями. Одначе розімкнути його без ключа ви вже не можете. Ось ваша записка в коробці, закриваєте коробку, навішуєте замок на петлю коробки і затискаєте скобу. Вона клацнула, в середині зубчик защепив виточку в скобі замка і не відпускає її назад. Ключ від замка лише у гоподаря замка. Якийсь посильний бере коробку із запискою в ній і несе до власника ключа. Зрозуміла схема. Трохи її ускладнимо.
Знову ця сама коробка. Два замки, котрі можна защепити стискуванням пальців на скобі. Ключ від вашого замка лише у вас. Ключ від іншого замка у вашого респондента. Ви десь зустрілися і ваш респондент дав вам свій замок в розімкненому вигляді.
Ось потреба стала відправити йому секретного листа. Пишете листа, вкладаєте в коробку, ще в коробку кладете свій замок у розімкненому вигляді, а на петлю коробки навішуєте замок респондента і защеплюєте його. В такому вигляді відправляєте коробку з кур’єром.
Ваш респондент отримує коробку, своїм ключем відпирає замок на петлі коробки, читає листа, пише відповідь, кладе лист в коробку і СВІЙ розімкнений замок, а на петлю коробки навішує ВАШ замок і защіплює його. Це такий собі поетичний образ обобічного (end-to-end) запирання повідомлення.
Опис далекий від математики, він більше поетико-драматичний, аніж технічний. Комусь і цього досить. Хоча може й далі читати – там буде цікава арихметика, а в самому кінці зауваження, щодо “сквазнова шЬІфраванія”. :)
Ррозділ другий. Генеруємо приватний і публічний ключі RSA.
Власне, до арихметики. Генеруємо RSA пару, що складається з приватного ключа й публічного ключа. В житті це виглядає доволі буденно: команда “ssh-keygen” виконує всю цю містику.
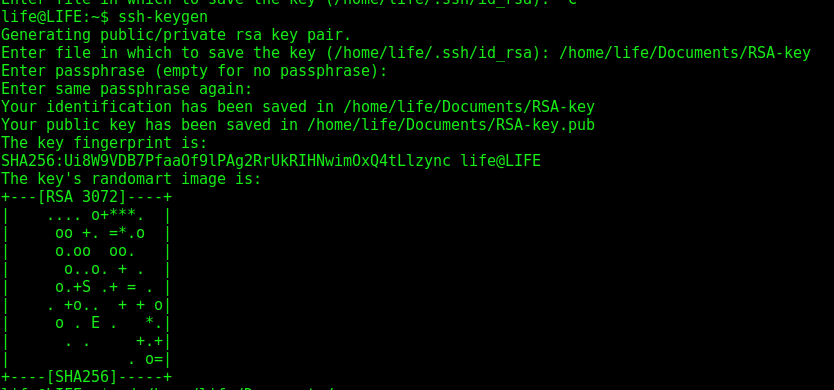
В результаті у вказааній директорії ми бачимо щойно згенеровану RSA пару
RSA-key
RSA-key.pub
RSA-key.pub виглядає теж доволі буденно:
ssh-rsa AAAAB3NzaC1yc2EAAAADAQABAAABgQDOxOs/B0YBkporptuPdKY1fJe+cSuQnUoyiinIj1tTokO7apLT8DG5g1hm6Q+rh5849uhD7YyvD85Ds4WVP5 wnhYnQ4EZGf1zsf1Qi0m/iCopr+mxwG2v5eIDuqCfmGDys4iq0ewWxWSzyNGK/6u5zTyb+NHd8mgntSbarg9uq/lc E26jkAHWNotJl58sIo8/GH/ToYHhMxX6f8gmSr81lbnT/bIy2JYPhourekq29oKRNXRami6uhM+EzdjDPZwR/CLwu NfHaNhAq1qpSWVoOC44OrzrUsTiznM52tW3dDXp2HcIyXfoihkaEQVvs5s/BR+2o6ibZPp9pcHjfdYrgWUP/Sz7S/ h3p/dK42YsSQVtiRqnQ1t9jpHPiE72GoDPx/0dvBJEqGmjnAZjtoQFtvl9PZ00+XxkRLOhPRn6b+ToHd1XH43ecIZ Dg6AtgJ+cfBnwYoJVBDIYfp4d+u7nopNHQJNc4RhCaIEDdTl5OmyviC4HNp9AhRsQgXhPFfUs=
Приватний ключ в декілька разів більший, і на вигляд схожий. І насправді це не букви, а числа. Для процесора, котрий займатиметься шифрацією/дешифрацією це лише число. Велетенські множники у сотні цифер довжиною, одначе ми з вами візьмемо не велетенські множники, а маленькі, щоби можна було з ними впоратися на папірцеві навіть без калькулятора і щоби ви зрозуміли концепцію раніше, аніж втомитеся це читати.
RSA пара починається з двох чисел – “p” і “q”. Коли ви генеруєте RSA пару, ваш комп навмання вибирає ці два числа. Грубо кажучи, процесор кілька мільйонів разів кидає кості, тасує результати, знову кидає, знову тасує і на місці “p” та “q” маємо велетенські навмання згенеровані числа, з котрих все й починається.
Нехай буде p=2 q=7
За допомогою цих двох множників ми отримаємо модуль, спільний для обох ключів – і приватного, і публічного. Назвемого його M. M= p*q = 2*7 = 14.
M=14
Нам треба знайти спільний дільник для ключа шифрування “e” - Ф(M) – де “Ф” функція Ойлера (Швейцарського математика 18-го століття, дивіться на десятимарковій швейцарській банкноті). Ф(M) = (p-1)*(q-1) = (2-1)*(7-1) = 1*6 = 6
Ф(M) = 6
А зараз розкладімо добуток p*q на ряд послідовних чисел (ми ж домовилися вище, що візьмемо маленькі числа, щоби можна було навіть подумки множити й ділити, а отже навіть від 1 до 9 ми називатимемо теж числами, хоч і, математично кажучи, - виглядають як цифри):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Якісь із цих чисел є спільними дільниками до M, а якісь ні. Точно можемо відповісти, що спільним дільником 14 є ті самі два співмножники 2 і 7. Також 1. Одиниця є спільним дільником для всіх чисел, то й її теж викидаємо.
1 – викреслюємо: бо ділить всіх (хоч і залишає те ж саме число в результаті).
2 – викреслюємо: бо в нашому випадку це первинний співмножник “p”
3 – залишається (бо ні з “p”, ні з “q” у взаємодію не вступає)
4 – викреслюємо: спільний дільник для “p” (4/2=2), логічно?
5 - залишається (бо ні з “p”, ні з “q” у взаємодію не вступає)
6 – викреслюємо, бо ділиться по модулю на наше число “p” (6/2=3)
7 - викреслюємо: бо в нашому випадку це первинний співмножник “q”
8 - викреслюємо, бо ділиться по модулю на наше число “p” (8/2=4)
9 - залишається (бо ні з “p”, ні з “q” у взаємодію не вступає)
10 - викреслюємо, бо ділиться по модулю на наше число “p” (10/2=5)
11 - залишається (бо ні з “p”, ні з “q” у взаємодію не вступає)
12 - викреслюємо, бо ділиться по модулю на наше число “p” (12/2=6)
13 - залишається (бо ні з “p”, ні з “q” у взаємодію не вступає)
14 - викреслюємо, бо ділиться по модулю як на число “p” (14/2=7), так і на “q” (14/7=2)
В результаті цього перебору, ми отримали ряд чисел, котрі НЕ мають спільних дільників з “M”. Назовімо для зручності СП – “СпівПервинні”.
3Тепер треба згенерувати ключ шифрування “e”. Формула Ойлера каже: e = (1 < e < Ф(M)).
За цією умовою із ряду СП чисел випадуть числа 9, 11, 13.
Залишаються 2, 3, 4, 5 (тому що 1<e<Ф(M)), але 2 і 4 ми викинули ще раніше, тому що вони спільні дільники як для “p” або “q”. Маємо тільки 3 і 5, що відповідають умові 1<e<Ф(M). Одначе 3 є спільним дільником для самого Ф(M), тобто 6. Відкидаємо також і це 3. Залишається 5.
Маємо публічний ключ для шифрування!
e = (5,14).
Як ви пам’ятаєте M=14 – спільний модуль для приватного й публічного ключа.
Зараз згенеруємо ключ для дешифрування – “d”. Це приватний ключ. Його окрім вас ніхто не має.
Для генерування приватного ключа, ми маємо вже все необхідне:
* число Ф(M) = 6
* число “e” = 5
* числа ряду M, по котрому ми пройдемося, перемножуючи на нього “e” послідовно збільшуючи кожен наступний множник на одиницю і ділячи на модуль Ф(M) (ділення на модуль, це ділення з остачею, хто забув перший клас середньої школи).
Ось так: e*1%Ф(M)
5*1%6=5
5*2%6=4
5*3%6=3
5*4%6=2
5*5%6=1<<< Одиниця в остачі
5*6%6=0
5*7%6=5
5*8%6=4
5*9%6=3
5*10%6=2
5*11%6=1<<< Одиниця в остачі
5*12%6=0
5*13%6=5
5*14%6=4
Кожен шостий (тому що Ф(М) = 6) цикл Ф(M) отримуємо ділення без остачі – 0.
Для ключа дешифрування “d” нам треба знайти такий множник, щоби він давав остачу 1.
Ось є один 5*5%6=1 і ось є другий 5*11%6=1 Оскільки 5 уже зайнята ключем шифрування e=(5,14), то нам залишається 11 із 5*11%6=1.
Тож, ключ дешифрування: d = (11,14)
Підіб’ємо підсумки цієї клопіткої справи:
шифруємо публічним ключем: e = (5,14)
дешифруємо приватним ключем: d = (11,14)
Розділ третій. Таблиця символів.
Для компа літери – це числа. Існує таблиця символів, називається вона ASCII – American Standard Code for Information Interchange, або Американський Стандартний Код для Інформаційного Взаємообміну – АСКІВ. Це офіційна таблиця, де вказано кожен символ латинського алфавіту і його числовий відповідник у десятковому форматі, двійковому і шістнадцятковому. А = 65, B = 66, C = 67 і так далі.
Як і в першому розділі, де ми штучно й умовно взяли дуже маленькі первинні числа 2 і 7, ми і в цьому розділі просто собі уявимо, шо A = 1, B = 2, C = 3 і створимо таку свою умовну таблицю АСКІВ.
A=1
B=2
C=3
D=4
E=5
F=6
G=7
H=8
I=9
J=10
K=11
L=12
M=13
N=14
O=15
P=16
Q=17
R=18
і так далі...
Розділ четвертий. Шифруємо і дешифруємо.
Ви хочете зашифрувати і послати текст LIFE.
У Числовому вигляді він такий: “12” “9” “6”, “5”
Ключ шифрування, нагадую – це публічний ключ, яким ви ділитеся з усіма, - e=(5,14)
Берете першу літеру 12 і підносите до ступеня 5, перше число публічного ключа.
12 в ступені 5 = 248832 (ну от бачте, навіть такі мізерні числа дають вже чималенькі добутки, а в реальному ж то житті там числа не 5 і не 14, а - сотні цифер в ряд!…)
12^5=248832. Тепер 248832 поділимо з остачею на 14.
248832 % 14= 10
Наступна літера I – 9
9^5 = 59049 % 14 = 11
Літера F – 6
6^5%14 = 6
Літера E – 5
5^5%14 = 3
В результаті 10 11 6 3, якщо перевести знову в літери, буде JKFC.
Оцей чудернацький текст “JKFC” і є ваше закодоване ключем RSA повідомлення, котре ви відправляєте своєму адресату.
Адресат його приймає і своїм ПРИВАТНИМ ключем його розкодовує. Нагадую: приватний ключ – d = (11,14)
Тест “JKFC” знову обертаємо в числа 10 11 6 3
Число 10 підносимо до ступеня 11 і ділимо з остачею на 14, і так далі з рештою чисел:
10^11%14 = 12
11^11%14 = 9
6^11%14 = 6
3^11%14 = 5
Знову повертаємо в літери – LIFE.
Розділ п’ятий. Ближче до реалій.
Все описане вище - правильне. Але має одну ваду: воно НЕ працює на “малих обертах”, як і двигун, котрому треба забезпечити мінімальні необхідні оберти, щоби він хоча б тиск мастила міг підтримувати у вкладках колінвала. Ви можете поволі провертати двигун руками, зупиняючи то тут, то там, аби прослідкувати весь алгоритм його роботи, одначе на цьому не поїдеш.
Точно так і тут: числа 2 і 7 занадто малі, щоби спрацювати з реальними ASCII кодами вашого тексту. В дійсності цифри настільки велетенські, що добуток утворює 2048 байтовий ключ – RSA-2048. А RSA-4096 – взагалі вже виглядає як дурні манери, бо навіть для RSA-1024 до кінця життя Всесвіту навряд чи який суперкомп зможе підібрати співмножники. RSA-2048 вже навантажує процесор, уявляєте що робиться в RSA-4096. І спробуйте підібрати які там були співмножники, що утворили ряд довжиною 2048 чисел (букви – числа), а спільні дільники “e” та “d” підібрати ще важче.
Та то все лірика. Розгляньмо реальний випадок на “мінімальних обертах” RSA алгоритму. Як підбирати числа “e”, “M” та “d” я описав вище, хочете повправлятися в арихметиці – прошу. Я вже показуватиму на готових числах, лише додам таблицю реальних ASCII кодів, а не тих спрощених-вигаданих з третього розділу.
Первинні числа (кинув дві кості, одна кістяшка лягла 6 догори, друга 1; ще раз кинув – 5 і 3, хай буде 61 і 53 ) - p=61, q=53
M=3233
Ф(М) = (p-1)*(q-1) = 60*52 = 3120
Знайшли спільний дільник публічного ключа - e=17
Знайшли спільник дільник приватного ключа d=2753
Маємо:
публічний ключ e = (17, 3233)
Приватний ключ d = (2753, 3233)
Таблиця кодів для алфавіту та інших символів.
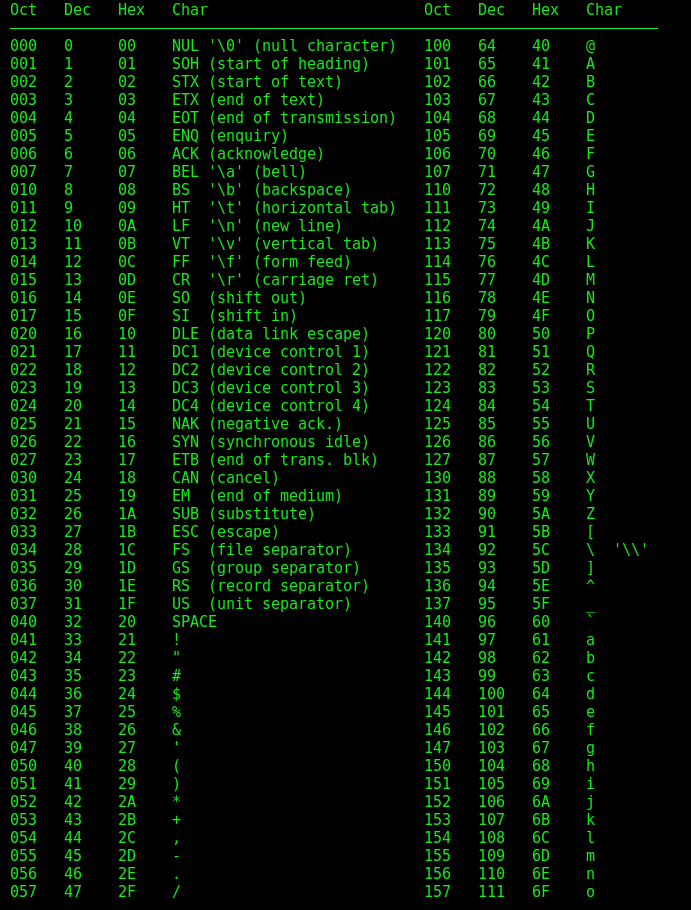
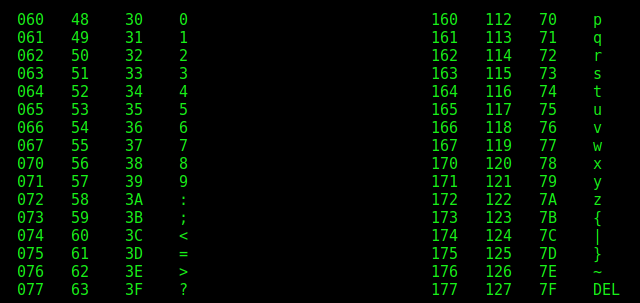
Розділ шостий. “Я пишу тобі листа”©.
Hello, my dear!
Переведімо в числові десяткові коди кожен символ: 72 101 108 108 111 44 32 109 121 32 100 101 97 114 33
Тепер зашифруємо публічним ключем, кожну літеру по порядку:
ЛІТЕРА ^ e % M = ШИФР
72^17%3233=3000
101^17%3233=1313
108^17%3233=745
108^17%3233=745
111^17%3233=2185
44^17%3233=678
32^17%3233=1992
109^17%3233=2271
121^17%3233=487
32^17%3233=1992
100^17%3233=1773
101^17%3233=1313
97^17%3233=1632
114^17%3233=2412
33^17%3233=1853
Текст вийшов ось такий:
3000 1313 745 745 2185 678 1992 2271 487 1992 1773 1313 1632 2412 1853
У файлі цей рядок виглядатиме як абракадабра із таблиці символів. Тому що 30 – це RS код (невидимий як і пробіл), 00 – кінець рядка (невидимий), 74 – J, 57 – 9 і так далі, хочете повправлятись, хай буде вам поживою для розуму. :)
Тобто ви побачите текст як у прикладі публічнорго ключа вище – щось таке “D85Ds4W/VP5wnhYnQ4EZ”...
Цей зашифрований текст відправляєте вашому адресату. Він його розшифрує за допомогою приватного ключа:
ШИФР ^ d % M = ЛІТЕРА
3000^2753%3233=72
1313^2753%3233=101
745^2753%3233=108
745^2753%3233=108
2185^2753%3233=111
678^2753%3233=44
1992^2753%3233=32
2271^2753%3233=109
487^2753%3233=121
1992^2753%3233=32
1773^2753%3233=100
1313^2753%3233=101
1632^2753%3233=97
2412^2753%3233=114
1853^2753%3233=33
Збираємо дешифровані числа в рядок:
72 101 108 108 111 44 32 109 121 32 100 101 97 114 33
Переносимо числа в літери, і маємо дешифрований текст:
Hello, my dear!
Розділ сьомий. Можливість частотного перебору
Так. Маючи потужний суперкомп можна методом частотного підбору здогадатися, які шифри стоять за літерами. А тому RSA не робить так, як показано вище. RSA алгоритм шифрує літери блоками. Знову ж для простоти прикладу я візьму маленькі блоки, не по 4 чи 8 літер, а дві досить.
Hello, my dear!
“He” “ll” “o,” ” m” “y “ “de” “ar” “!” пробіли, кома, оклик – повноправні члени тексту і мають свої коди.
“72101” “108108” “11144” “32109” “12132” “100101” “97114” “33”
Але тут знову бракує “обертів”. Тому первинні множники “p” та “q” треба робити ще більшими! Я вже цього не робитиму, бо мені просто лінь, а ви втомилися, а хто не втомився вже готовий до заключного розділу “Частини першої”.
Рорзділ восьмий. Політико-ліричний.
Ось ви з вашим другом (респондентом) приходите до магазину купити два замочки й під час купівлі радісно ділитеся з продавцем ідеєю, що осяйнула ваші світілі голови. Продавець пропонує вам двом послуги свого малого сина. За невеличку символічну плату, він возитиме між вами цю коробочку, на новому велику заодне кататиметься. А ви такі радісні, - от як добре все складається, і замки купили, і посильного вже маємо, ще й від каси не відійшовши. Лише хитрий продавець усміхається собі у вуса, приховавши непомітно по копії ключа до ваших замочків… :)
Встановлюєте ви такий собі телеграм чи вайбер, чи вацап, реєструєтеся, даючи свій номер телефону (хоч це й не важливо). Сервер вашого месинджера, котрий бігатиме між вами і вашими респондентами прудким хлопчиком на велику з коробочкою, генерує (видає замки з ключами) вам ключі шифрування. Сервер вам генерує, а не ваш телеграм застосунок – зажирне задоволення генерувати ключі процесором смартфона, ніхто вам не писатиме купу програмного коду, шоби ваш месинджер сам собі генерував шифри, та й нашо? Он всі наші сервери до ваших послуг! Ми згенеруємо вам ключі і прикріпимо до вашого пристрою. Ми працюємо для вас! (лохи! тсс...)
Так. Розшифрувати обмін, зашифрованй RSA неможливо, принаймні можна пробувати доки Сонце не сколапсує в білого карлика. Однак, той хто для вас згенерував ключі, той залишив собі копії. І то вже ваші проблеми, який сервіс обирати, вони всі однакові, шо телеграм, шо вайбер, шо вацап. Справа лише в тому, шо телеграм з вайбером належать кацапам через підставні картонні манекени. До вацапа доступ кгб ускладнений, може якшо Цукерберга добре попросити. До скайпа – якшо Ґейтса добре попросити, він добра душа – дасть.
Google Hangouts – те ж саме: його можуть читати як я й сказав, ФБР запитає в суду ордер і прочитає все. Ключі шифрування нікуди не діваються, копії ключів сервіс зберігає теж.
А обирати того ХТО тебе читатиме – КГБ чи ФБР – тобі %юзернейм%!
Оці всі красиві обгорточки “ваше листування захищене наскрізним шифруванням” – це лише красива обгорточка. Ще й переклад запозичили у кацапів, end-to-end encryption аж ніяк не схоже на “свозноє шЬІфрованіє”, це “обобічне/двобічне шифрування”, де кожен з двох учасників шифрує обмін. Шо таке “сквозноє” не знаю.